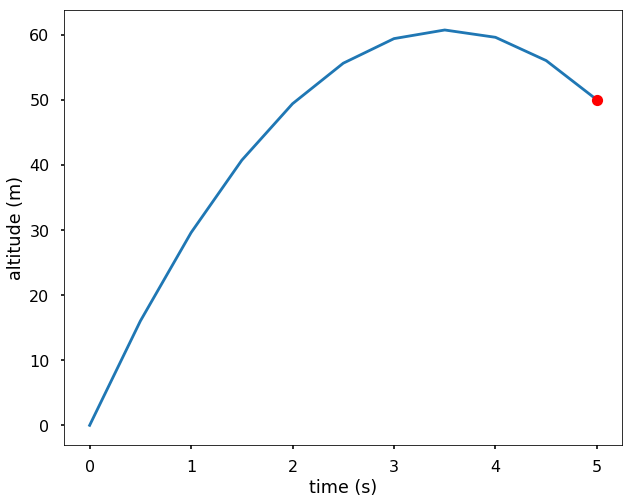
Boundary Value Problem Using Finite Difference Method

The script can set either the periodic boundary conditions described in Example 1 or can set the inflowoutflow boundary condition s described in Exercise 2. In mathematics in the field of differential equations a boundary value problem is a differential equation together with a set of additional constraints called the boundary conditions.

Finite Difference Method Python Numerical Methods

1 This Matlab script solves the one-dimensional convection 2 equation using a finite difference algorithm.

. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Formulation of Finite Element Method for 1-D Poisson Equation Mrs. Here ψ i denotes the basis functions and u i denotes the coefficients of the functions that approximate u with u hThe figure below illustrates this principle for a 1D problem.

The method uses a distance function to the true boundary to enforce Dirichlet boundary conditions on the non-aligned mesh faces therefore shifting the location where boundary conditions are imposed. The equation is defined on the interval 0 π 2 subject to the boundary conditions. Y y 0.

21 the boundary conditions given by Eq. In this method various. We can obtain from the other values this way.

Y 0 0. For an accurate local approximation the trust-region should be large and for an approximation valid only close to the current point it should be a small one. University Jhunjhunu Rajasthan India Abstract -This paper focuses on the use of solving electrostatic one-dimension Poisson differential equation boundary-value problem.

We will solve a. So with this recurrence relation and knowing the values at time n one can obtain the. The diffusion miniapp found in the miniappsshifted directory demonstrates the capability to formulate a boundary value problem using a surrogate computational domain.

F x y y a x b dx d y 2 2 1. 211 represents a system of N linear algebraic equations with N. Here the linear basis functions have a value of 1 at their respective nodes and 0 at.

To solve this equation in MATLAB you need to write a function that represents the equation as a system of first-order equations a function for the. Equation 215 in conjunction with Eq. Y π 2 2.

. Rattlesnake Wang et al 2018 has the ability to simulate complex pebble-bed problem using SN angle discretization and Discontinuous Finite Element Method DFEM spatial discretization and it implemented pebble tracking transport algorithm to reduce the load of calculation. Boundary value problems arise in several branches of physics as any.

The algorithm will terminate when both the infinity norm ie max abs value of the Lagrangian. It reflects the trust the algorithm puts in the local approximation of the optimization problem. The trust radius is automatically.

Finite Difference Method applied to 1-D Convection In this example we solve the 1-D convection equation U t u U x 0 using a central difference spatial approximation with a forward Euler time integration Un1 i U n i t un i δ2xU n i 0. We will look at the eigenvalues of both cases. For the nodal system depicted in Fig.

The finite difference method is used to solve ordinary differential equations that have conditions imposed on the boundary rather than at the initial point. This approximation is the Forward Time-Central Spacemethod from Equation 111 with the diffusion terms removed. However there is no efficient acceleration method in Rattlesnake perhaps suffering from the limitations.

In this chapter we solve second-order ordinary differential equations of the form. Solve a second-order BVP in MATLAB using functions. Rastogi Research Scholar Department of Mathematics Shri.

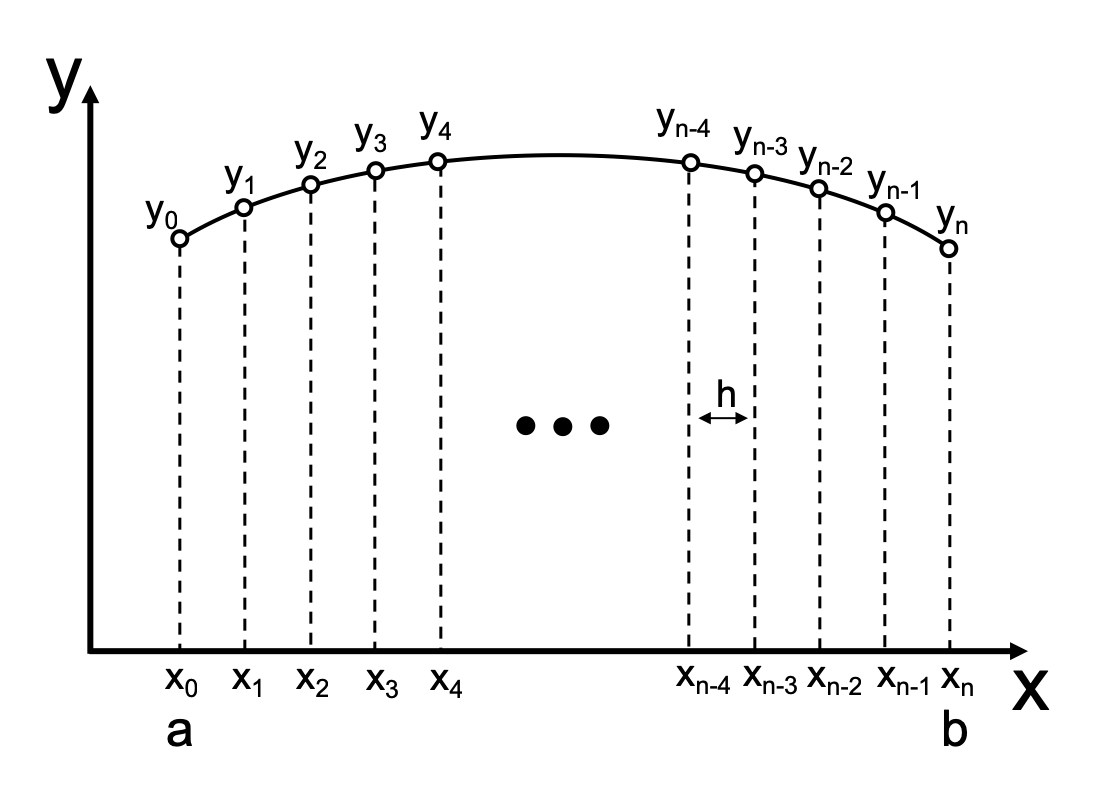
In the finite difference method since nodes are located on the boundary the Dirichlet boundary condition is straightforward to apply. Another way to solve the ODE boundary value problems is the finite difference method where we can use finite difference formulas at evenly spaced grid points to approximate the differential equationsThis way we can transform a differential equation into a system of algebraic equations to solve. This is an explicit method for solving the one-dimensional heat equation.

For this example use the second-order equation. There are various finite difference formulas used in different applications and three of these where the derivative is calculated using the values of two points are presented below. 22 may be written as 215 ϕ 1 ϕ L ϕ N ϕ R.

In finite difference approximations of this slope we can use values of the function in the neighborhood of the point xa to achieve the goal. The derivative at xa is the slope at this point. Using a forward difference at time and a second-order central difference for the space derivative at position we get the recurrence equation.

These problems are called boundary-value problems. U could for instance represent the temperature along the length x of a rod that is nonuniformly heated. Where.

Finite Difference Methods An Overview Sciencedirect Topics

Finite Difference Method An Overview Sciencedirect Topics

Finite Difference Method Python Numerical Methods

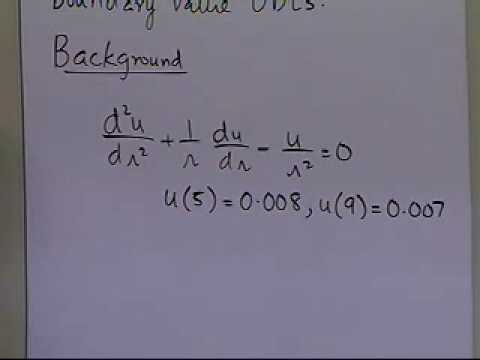
Chapter 08 07 Lesson Finite Difference Method For Solving Odes Example Part 1 Of 2 Youtube

Approximating The Jacobian Finite Difference Method For Systems Of Nonlinear Equations Youtube

Finite Difference Method Initial Value Problem Mathematics Stack Exchange